Hello & Welcome

I Am

About Me

AI with social-purpose. I work across fields in generative AI and sociotechnical foresight, to develop solutions for global challenges, equity and safety, participation and African AI leadership.

Generative Machine Learning
Weather & Climate
Sociotechnical AI
Transformation

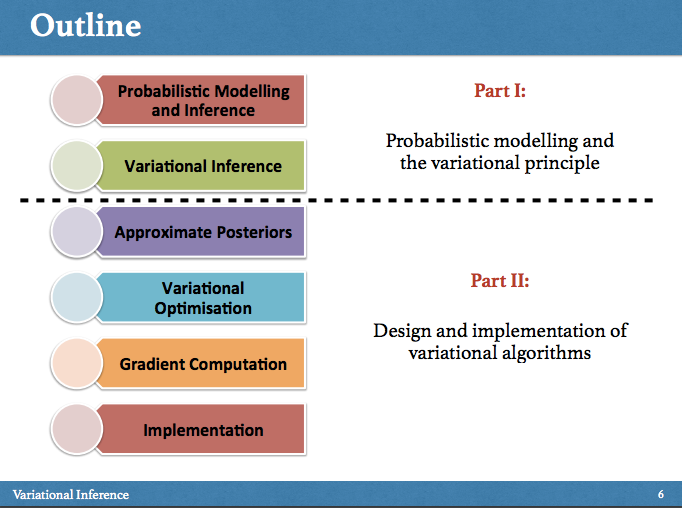
I am a scientist and engineer in the fields of statistical machine learning and artificial intelligence. I am most interested in research that combines multiple disciplines and views of machine learning and its applications. I shape my efforts around three conceptual pillars: Probabilistic Foundations of Learning and Intelligence, Addressing Global Challenges, and Transformation. I work towards developing methods focussed on probabilistic reasoning that lead to systems for agent-based decision-making. I work towards the application of machine learning to global challenges in healthcare and environment, and towards social Transformation that supports greater diversity, responsibility, and freedom. I love exploring and writing about the connections between different computational, epistemological, and social paradigms and maintain a blog at blog.shakirm.com.

I am a Director for research at Google DeepMind in London; I joined DeepMind as a small startup in 2013. I am also a founder and Chair of the Board of Trustees of the Deep Learning Indaba, a non-profit whose mission is to Strengthen African Machine Learning and Artificial Intelligence. I'm an Associate Fellow at the Leverhulme Centre for the Future of Intelligence at the University of Cambridge, and an Honorary Professor in the Department of Computer Science at University College London (UCL).

I was a programme chair for DALI2019, a programme co-chair for ICLR2019, the Senior Programme Chair for ICLR2020, the General Chair for ICLR2021, and a co-General Chair for NeurIPS 2022. I am a member of the Royal Society’s Diversity and Inclusion Committee (2020-2025). I am a member of the Board of Directors of ICML, ICLR, and NeurIPS.

Before moving to London, I held a Junior Research Fellowship from the Canadian Institute for Advanced Research (CIFAR) as part of the programme on Neural Computation and Adaptive Perception. I was based in Vancouver at the University of British Columbia in the Laboratory for Computational Intelligence (LCI) with Nando de Freitas. I completed my PhD with Zoubin Ghahramani at the University of Cambridge, where I was a Commonwealth Scholar to the United Kingdom and a member of St John’s College. I am from South Africa, and completed my previous degrees in Electrical and Information Engineering at the University of the Witwatersrand, Johannesburg.

Talks

Links to overviews, slides and videos of some of my talks.

AI for Science Summit

Generative Science

Stanford HAI Fall Conference

Responsibiilities of the Pioneer

ICML 2023 Keynote

ML with Social Purpose

AISTATS 2023

Elevating our Evaluations

Climate Informatics 2023

Generative Models

Tackling Clim. Change 2021

ML for Net Zero

NAACL 2021 Keynote

Generating Reality

NeurIPS2020 BioRL

Pain and ML

NeurIPS2020 ML-RSA

Through the Eyes of Birds and Frogs

TechAide 2020

Imaginations of Good, Missions for Change

Queering Machine Learning

Queer In AI @ ICML2020

Bayesian Learning (4 Parts)

MLSS 2020

Decolonising Artificial Intelligence

Intercultural Dig. Ethics 2019

Machinery of Grace

TEDxLSTM 2019 Liverpool

Case Study in Data Science and AI: Predicting Organ Damage in Hospitals

Edinburg Data Science CDT

Racialised Lives and the Life Beyond

Equality in Science 2019

Machine Learning for Environmental Grand Challenges

Cam Environmental Risk

Deep Generative Models

UAI Tutorial 2017

How do We Support Underrepresented Groups

Royal Society Diversity Conf.

Planting the Seeds of Probabilistic Thinking

MLSS 2018, Madrid

Variational Inference

NeurIPS 2016 Tutorial

Observations and Inspirations

Sheffield ML Retreat 2017

Variational Inference

Imperial ML Tutorials

Research Areas & Activities

I have a broad range of interests in Machine learning and artificial intelligence that takes a broad view of the field and the many other areas it shapes and that in turn shapes it.

Probabilistic Modelling

I seek to describe problems and processes using the language of probability to make consistent reasoning from evidence.

Bayesian Analysis

Develop methods and algorithms for approximate Bayesian inference and high-dimensional inference and integration.

Variational Inference

I've spent much timestudying a specific class of distributional approximation methods and its applications in practice.

Global Challenges

Tackling big problems in healthcare, weather and climate.

Sociotechnical Systems

Crtical research practuce to understand how ML shapes and is shaped by society.

Transformation

Committed to thought and action towards social Transformation that supports greater diversity, responsibility, and freedom.

Community and Leadership

Action at the grassroots, community service, board membership, advisory service.

Engagement and Policy

Supporting knowledge transfer in evidence gathering, policy development, and broader engagement.

Writing and Teaching

I develop my craft of writing through my blog, and give regular talks on different aspects of my work.

Media

Podcasts, Interviews, Media coverage

This Week in ML and AI. Live conversation with Sam Charrington.
Nature Machine Intelligence book review. Domesticating the techno-racial project.
The Comb on BBC Africa. Racist AI.
MIT Tech Review. The problems AI has today go back centuries.
New York Times, London Lab Advances Use of A.I. in Health Care, but Raises Privacy Concerns.
TedX LSTM, Machinery of Grace.
BBC Radio 4 & World Service, Will AI kill development?
BBC Click, What is the Deep Learning Indaba

Roles, Leadership & Experience

A summary of some of my roles and educational path.

2013 -

Research Director

DeepMind, London. Director for science, technology and society.

2017 -

Co-founder and Chair of the Board of Trustees

Deep Learning Indaba

2020-2024

Associate Fellow

Leverhulme Centre for the Future of Intelligence, University of Cambridge.

2020-2024

Honorary Professor

Department of Computer Science, University College London (UCL)

Boards and Committees

2023-2025

Oversight Board, Ada Lovelace Institute

2022-2025

Board of Directors, Neural Information Processing Systems Foundation

2022-2025

Chair, International Scientific Advisory Committee for the Pan-Canadian AI Strategy

2019-2024

Board of Directors, International Conference on Learning Representations

2020-2025

Royal Society Diversity and Inclusion Committee

2011 - 2013

Junior Research Fellowship

Fellowship from the Canadian Institute for Advanced Research (CIFAR) at the University of British Columbia, Vancouver. Mentor, Nando de Freitas

2007 - 2011

PhD in Statistical Machine Learning

St John's College, University of Cambridge. Thesis: Generalised Bayesian Matrix Factorisation. Supervisor: Zoubin Ghahramani.

2006 - 2007

Master of Science in Engineering (MSc(Eng)), Distinction

University of the Witwatersrand, Johannesburg. Dissertation: Dynamic Protein Classification: Adaptive Models based on Incremental Learning Strategies. Supervisor: Tshilidzi Marwala.

2002 - 2005

Bachelor of Science in Information Engineering (BSc(Eng)), Distinction

University of the Witwatersrand, Johannesburg. Chancellor's Medal, SIAMM Gold Medal, Bernard Price Prize.

Past Boards and Committees

2019-2023

Board of Directors, International Conference on Machine Learning

2020-2023

Partnership on AI, AI and Shared Prosperity Initiative

2019-2020

Royal Society, Digital Technology and the Planet

Machines

Dearest, note how these two are alike: This harpsichord pavane by Purcell And the racer’s twelve-speed bike. The machinery of grace is always simple. This chrome trapezoid, one wheel connected To another of concentric gears, Which Ptolemy dreamt of and Schwinn perfected, Is gone. The cyclist, not the cycle, steers. And in the playing, Purcell’s chords are played away. So this talk, or touch if I were there, Should work its effortless gadgetry of love, Like Dante’s heaven, and melt into the air. If it doesn’t, of course, I’ve fallen. So much is chance, So much agility, desire, and feverish care, As bicyclists and harpsichordists prove Who only by moving can balance, Only by balancing move. --Michael Donaghy

Events

A log of things I'm up to and upcoming events.

Upcoming

Feb 2024: Speaking at Connect and Collaborate event for the 2023/34 Commonwealth Scholars.
Sept 2024: Excited to be at the 2024 Indaba.

2023

Dec 2023: Spoke at the AI for Science Summit hosted by the Accelerate Programme for Scientific Diiscovery.
Oct 2023: Giving a keynote at the Standford HAI Fall conference on New Horizons in Generative AI.
September 2023: I'll be at this year's Deep Learning Indaba is in Accra.
July 2023: Keynote at ICML 2023 in Hawaii
26 April 2023: Keynote at AISTATS2023 on Elevating our Evaluations: Technical and Sociotechnical Standards of Assessment in Machine Learning
19 April 2023: I'll be joining the MSt on AI Ethics Meetup to Talk about sociotechnical AI.
17 April 2023: Keynote at Climate Informatics on Generative Models for Climate Informatics.
March 2023: Meeting the Board of the Turing Institute to discuss topic of diversity and inclusion in the field.
Feb 2023: Supporting the AI Ecosystem and engagement advisory group for the Turing Institute's strategy renewal.
23 Jan 2023: Speaking on a panel on Ethical AI at the UCLA graduate women in computer science seminar.

2022

Dec 2022: I'll be a General Chair for NeurIPS 2022 in December, alongside Sanmi Koyejo.
September 2022: At the Heidelberg Laureate Forum, speaking on a panel on AI.
September 2022: On the final slection panel for the UKRI programme director on Responsible AI.
August 2022: At the Deep Learning Indaba, back in-person, in Tunis.
16 June 2022: Speaking in Cambridge at the AI4ER workshop on Environmental Justice and AI.
16 June 2022: Speaking at New Scientist Live.
14 June 2022: In Edinburgh, contributing to the workshop on Ethics of Care in AI and Data practice.
March 2022: Joined as a member of International Scientific Advisory Committee (ISAC) for the Pan-Canadian AI Strategy.
March 2022: Speaking at the ALBA Network on Racism in Statistical Sciences.
Jan 2022: Joined the NeurIPS Board.

2021

3 Nov 2021: Workshop on Intercultural Digital Ethics
18 October 2021: Respondent to Prof. Ruha Benjamin's Cambridge Tanner Lecture
23 July 2021: ICML2021 Woprkshop on Tackling Climate Change with Machine Learning
15 July 2021: Eastern European Machine Learning School
7 July 2021: UCL Diversity in Statistics
16 June 2021: Khipu Panel on Algorithmic Bias
16 June 2021: Turing Legacy Event. Breaking the code: Alan Turing’s legacy in 2021
14 June 2021: CogX Ethics Stage: Queer Tech and Designing for Diversity.
8 June 2021: Keynote at NAACL-HLT 2021 on Generating Reality.
21 May:Liverpool Museums, Opening of the Museum's new exhibition, AI: More than Human.
17 May: BBC AI and ML Community.
14 May: Alumni Series, Cambridge Computational and Biological Learning Laboratiry.
7 May: Hosting a panel on Values in Science and Engineering at the Science and Engineering of Deep Learning Workshop at ICLR2021.
3-7 May: I'm the General Chair for ICLR 2021
19 April: Fields Institute Lecture Series at the University of Toronto
23 March: AI UK COnference, Panelist on Doing Better in Data Science.
26 January: Upsalla University

2020

12 December 2020: Talk and Panel at the NeurIPS2020 Workshop on Biological and Artificial Learning, and a panel at the Workshop on Navigaating Broader Impacts of AI Research.
11 December: Talk and Q&A at the NeurIPS2020 Workshop on Meta-analyses, Reviews and Surveys
8 December 2020: Helped to organise aand then hosting the first Workshop on Muslims in ML.
3 December:Panel for the Royal Society Digital Technology and Planet Sessions.
23 Noveember: Looking forward to taking part in a panel at the Pembroke College Stokes Society at the University of Cambridge.
12 November: Talk and Q&A at the TechAIDE 2020 AI4Good Conference.
26 October 2020: Giving a talk on Decolonial for groups at the University of Amsterdam
3 October 2020: Season for ICLR2021 begins. I'm the General Chair for ICLR2021 and we are virtual again.
3 October 2020: Excited and nevous to do a live conversation with Sam Charrington at TWiML-Fest2020.
30 September 2020:Giving an PAI impule talk on Decolonial AI
3 September: I'm the MC for the Finals of the 2020 Africa Prize.
20-21 Aug: Speaking at the first Google AI India Summer School. Indonesia Machine Learning School.
3-8 August 2020: I’ll be speaking at the Indonesia Machine Learning School.
14 July 2020: Excited to share a talk on Queering Machine Learning and also hosting a fireside chat with Bisi Alimi at Queer in AI at ICML2020.
9 July 2020: So much fun hosting fireside chats. Fireside with Yoshua Benjio for EEMLS2020,
June 2020: Excited to finally have the opportunity to visit Tuebingen and speak at the MLSS2020 on Bayesian Analysis. Virtual, but still great!
3 June 2020. Joined a great panel on Data and Delusion after COVID-19 as part of the seminar series hosted by the University of Johannesburg,
26-30 April 2020: I’m very excited to be the Senior Programme Chair for ICLR2020 and take our conference to Ethiopia.We took the conference virtual and think it was a great success.
March 2020: Happy to support a new conference on Healthcare, Inference and Learning (ACM CHIL), and the machine learning track.
7 & 9 January 2020: Will be giving visiting and giving a talk at Lund University in Sweden and then in Copenhagen.
January 2020: I officially will take a role as a member of the Royal Society Diversity Committee and will participate in this committee for the next 3 years.

2019

10 December 2019: Speaking at the Intercultural Digital Ethics Symposium in Oxford.
16 November 2019: Speaking at TEDxLSTM in Liverpool on Machinery of Grace. 1 November: Speaking at the Edinburg Data Science CDT research day.
31 September 2019: In Cambridge to speak about Machine Learning for Environmental Grand Challenges, and the launch of the AI for Environmental Risk CDT in Cambridge.
17 September 2019: I’ll be at the Royal Festival Hall leading a session on day 2 of the 2019 Global Grand Challenges Summit
25-31 August 2019: Our 3rd year of the Deep Learning Indaba takes me to Nairobi for what should be our best Indaba yet.
31 July 2019: So excited to see the release of our paper in Nature on A clinically applicable approach to continuous prediction of future acute kidney injury.
17 July 2019: Speaking at the Machine Learning Summer School in London on Variational Inference.
18-21 June 2019: Speaking at the CFI’s “Kinds of Intelligence 2: Machine Minds” conference in Cambridge.
17 June 2019: Humbled to have been elected to the Board of Directors for the IMLS that oversees the ICML conference.
4 June 2019: Speaking at the Liverpool School of Tropical Medicine’s Equality in Science Symposium (LSTM EiS). 26 April 2019: Super excited to go to Ghana to speak at the IndabaXGhana.
6 April 2019: Was part of the interviewees for this documentary on AI and Development in Africa on the BBC World Service and BBC Radio 4.
23 March 2019: I’ll be speaking at the Imperial College Coding in Medicine Society’s annual conference. 7
March 2019: I’ll be supporting African startup innovators at Pitch@Palace Africa 3.0.
18-22 February 2019: Excited to make progress in AI for Social Good at a workshop in Dagstuhl.
7 January 2019: Giving a tutorial at the Machine Learning Summer School in Stellenbosch South Africa, and taking the opportunity to give a shorter version of my lectures on Planting the Seeds of Probabilistic Thinking.
3-5 January 2019: I’m the programme chair for DALI 2019 happening in George, South Africa.

2018

November 2018: Will be participating in the Royal Society annual diversity conference, this years theme of creating diverse leadership in a research environment.
October 2018: Looking forward to meeting the London ML community – I’ll speak at the London Machine Learning Meetup. September 2018: I’m happy to be one of the Programme Chairs for ICLR 2019 in New Orleans.
September 2018: Can’t wait to see our second year of the Deep Learning Indaba come together, continuing our work to strengthen African machine learning.
August 2018: I’ll be giving three lectures on the theme of Bayesian Deep Learning at the 2018 Machine Learning Summer School in Madrid.
July 2018: Will be speaking at the 2018 ISBA World Meeting in Edinburgh.
June 2018: Looking forward to speaking at the 4th Research and Applies AI Summit (RAAIS 2018) here in London.
April 2018: I’ll be at DALI2018, giving a keynote talk, speaking at the workshop on Generative models and RL, and organising another workshop on Goals and Principles of Representation Learning. March 2018: Will be giving the lecture on unsupervised learning and generative models as part of the UCL course on Advanced Deep Learning and Reinforcement Learning.
Feb 2018: Happy to speak at the launch of the Imperial College Machine Learning Society, and the first conference of the Imperial Coding in Medicine society.
January 2018: I’ll be a Publications chair for ICML2018, and the Tutorials chair for UAI2018.

2017

November 2017: I’ll be an area chair for AISTATS 2018 and ICLR 2018.
October 2017: More than excited to speak at the launch of the Imperial College Machine Learning Initiative, their university wide initiative to unify and strengthen their machine learning leadership.
September 2017: Months of work finally coming together at the 1st Deep Learning Indaba, in Johannesburg.
August 2017: Giving the UAI2017 Tutorial on Deep Generative Models.
August 2017: Organising the ICML2017 Workshop on Implicit Generative Models.
June 2017: Speaking at the Sheffield Machine Learning Group retreat on ‘Observations and Inspirations: Mutual Inspirations between Cognitive and Statistical Sciences’.
May 2017: Speaking at the Gatsby-Kakenhi workshop on ‘Plausible Reasoning in Artificial Agents’.
January 2017: I’ll be an area chair for ICML 2017 and NIPS 2017.

2016 and prior

December 2016: Will be discussing 4 papers at NIPS 2016.
August 2016: I’ll be speaking at the NIPS 2016 Workshop on Bayesian Deep Learning.
August 2016: I’ll be an area chair for ICLR 2017.
August 2016: I gave a tutorial at the 2016 Deep Learning Summer School in Montreal on ‘Building Machines that Imagine and Reason: Principles and Applications of Deep Generative Models’.
June 2016: With David Blei and Rajesh Ranganath, we’ll be giving a tutorial at NIPS 2016 entitled ‘Variational Inference: Foundations and Modern Methods’.
March 2016: I am one of the organisers of the ICML 2016 Workshop on Data-efficient Machine Learning.
August 2015: I am one of the organisers of the the NIPS 2015 Workshop on Advances in Approximate Inference.
January 2015: I’ll be an Area Chair for NIPS 2015.
September 2014: We’ll be at NIPS to discuss our paper on ‘Semi-supervised learning with Deep Generative Models’.
August 2014: I am one of the organisers of the NIPS 2014 Workshop on Advances in Variational Inference.
June 2014: I gave a talk at ICML in Beijing on our paper on ‘Stochastic Backpropagation and Approximate Inference in Deep Generative Models’.
…